

#Moment of inertia formula hollow cylinder how to#
If you are new to structural design, then check out our design tutorials where you can learn how to use the moment of inertia and section modulus to design structural elements such as. The process involves adding up the moments of infinitesmally thin cylindrical shells. W z 5 m m ( 100 m m) 2 6 + 100 m m ( 5 m m) 3 6 100 m m. The parallel moment of inertia is half the mass times. The expression for the moment of inertia of a hollow cylinder or hoop of finite thickness is obtained by the same process as that for a solid cylinder.
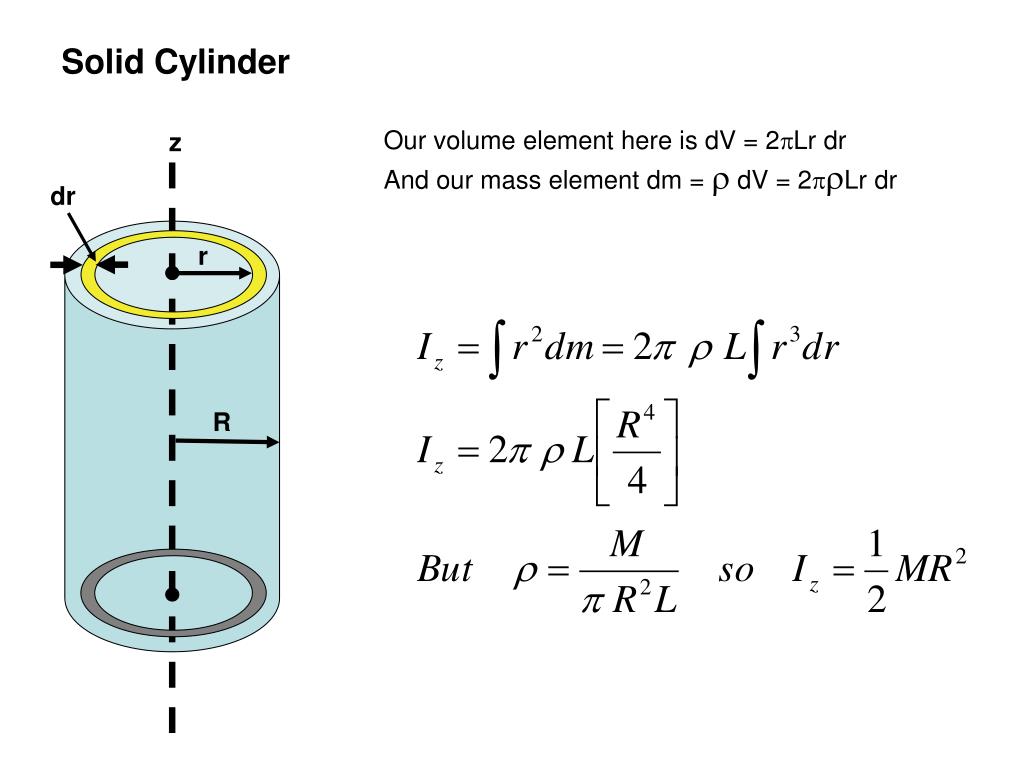
For a uniform solid cylinder, the moments of inertia are taken to be about the axes passing through the cylinders center of mass. These are just a few examples, and the moment of inertia formulas can. If the amount of friction is only enough to cause the cylinders to roll without slipping then all I said above is true but if you have less friction then the cylinders will just slid down the ramp and have the same speed. The mass moment of inertia measures the extent to which an object resists rotational acceleration about a particular axis, and is the rotational analog to mass. Hollow Cylinder (Rotating about Its Axis): For a hollow cylinder rotating about an axis coinciding with its axis of symmetry, the moment of inertia is given by: I m R2 where I is the moment of inertia, m is the mass of the cylinder, and R is the radius of the cylinder. Mass and radius of the cylinders should not matter. This means either increasing the length of the ramp or increasing the angle. To make this effect more noticeable is to increase the height that the cans are released from. The effect will be much less noticeable as it is will be harder to create rotation among the gas to the point if you consider the gas to be an ideal gas then there will be almost no difference. If it is a gas than it gets more complicated. This really depends on a couple different things, If the deodorant is a gas or if it is solid, what you mean by noticeable and what type of friction there is.įor the first part if you are comparing a solid deodorant than the solid deodorant can will always be sqrt(3)/2 faster than the empty can (a simple conservation of energy problem). The shallower the ramp is, the more the can has to rotate for a given drop in height, and so the more clear the difference is between a can whose motion is dominated by angular momentum (empty can) versus another whose motion is dominated by linear momentum (full can).
#Moment of inertia formula hollow cylinder full#
Had the liquid been much thicker, the result would be much different, but in this case, the difference in speed between the two bottles was obvious.įor the latter part of your question, the inclined plane is what forces the can to rotate - if you just dropped them, moments of inertia wouldn't factor in at all, and the full and empty cans would drop at very close to the same rate. Also, friction between the water and the bottle wasn't enough to make much difference. However, being much more massive than the bottle, the water contributed much more to the acceleration than did the bottle itself. What was also clear is that for a low-viscosity fluid like water, there wasn't enough friction for the water to "spin up" within the bottle - it all stayed on the bottom half of the bottle throughout the journey, so the water added nothing to the moment of inertia about the bottle's axis. The empty bottle behaved as you would expect an empty cylinder to, rolling slower than the full bottle.
I just did an experiment, rolling two identical transparent bottles, one empty, the other about half full, down about a 15-degree ramp. The assumption I'm making is that the fluid has a viscosity close to that of water, since the deodorant is mostly water, and by simply shaking a can of it we can tell it's not terribly viscous - it shakes like water in a can. Figure 10.6.1: (a) A barbell with an axis of rotation through its center (b) a. From this result, we can conclude that it is twice as hard to rotate the barbell about the end than about its center. Here we have the can, which is rolling, and the fluid, which is basically just falling. In the case with the axis at the end of the barbellpassing through one of the massesthe moment of inertia is.
That is, a solid cylinder will roll down the ramp faster than a hollow steel cylinder of the same diameter (assuming it is rolling smoothly rather than tumbling end-over-end), because moment of inertia depends on the distribution of mass, with mass further from the axis of rotation contributing more to moment of inertia than mass closer to the axis.īut that's only part of what's in play here. (Look at the cone from above it looks just like a disc, and indeed it has the same radial mass distribution as a uniform disc.As you say, "we know that hollow cylinders are slower than solid cylinders when rolled down an inclined plane".


 0 kommentar(er)
0 kommentar(er)
